4 基本计算规则

学习目标:

掌握时间复杂度的计算规则

4.1 时间复杂度的6条基本计算规则

1 基本操作，即只有常数项 简单来说：没有数量规模，就执行一次 时间复杂度：O(1)

2 顺序结构，时间复杂度按加法进行计算 简单来说：一步一步的执行下去，类似上面的方法二 时间复杂度：O(n)

3 循环结构，时间复杂度按乘法进行计算 简单循环：就是批量执行多次，类似上面的方法一： 时间复杂度：O(n3)

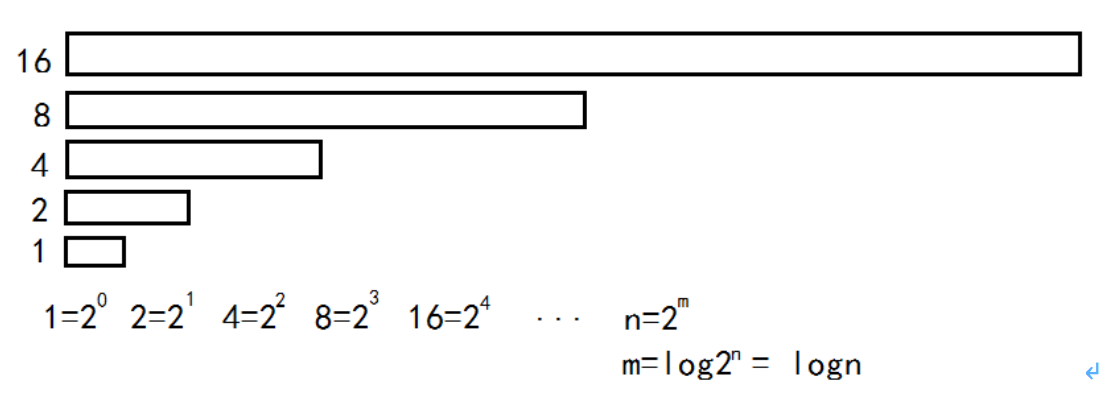
递归循环：重复同样的动作的重复次数 时间复杂度O(logn)

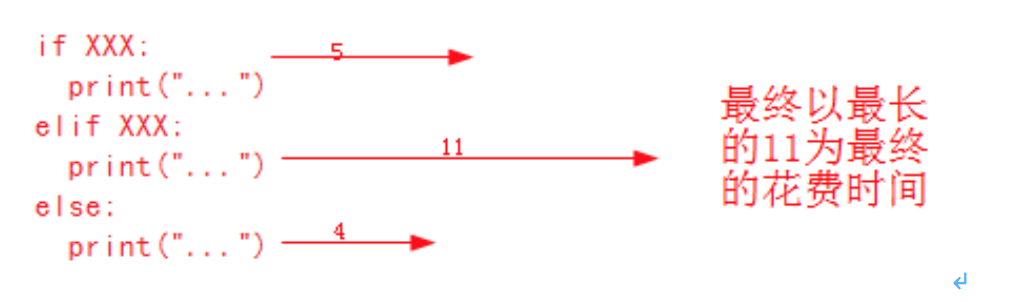
4 分支结构，时间复杂度取最大值 简单来说：就是多分支if语句，找一个时间最长的作为标准的时间

5 判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略

6 在没有特殊说明时，我们所分析的算法的时间复杂度都是指最坏时间复杂度

4.2 计算时间复杂度

1 第一次尝试的算法核心部分

for a in range(0, 1001):
    for b in range(0, 1001):
        for c in range(0, 1001):
            if a**2 + b**2 == c**2 and a+b+c == 1000:
                print("a, b, c: %d, %d, %d" % (a, b, c))

时间复杂度：

T(n) = O(n*n*n) = O(n³)

2 第二次尝试的算法核心部分

for a in range(0, 1001):
    for b in range(0, 1001-a):
        c = 1000 - a - b
        if a**2 + b**2 == c**2:
            print("a, b, c: %d, %d, %d" % (a, b, c))

时间复杂度：

T(n) = O(n*n*(1+1)) = O(n*n) = O(n²)

由此可见，我们尝试的第二种算法要比第一种算法的时间复杂度好的多。